Home
What is Sudoku?
How to play
Basic Techniques
More Advanced

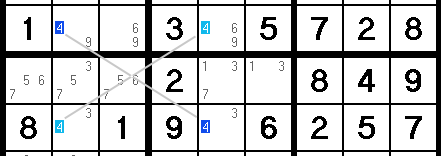
X Wing

An X Wing is a technique for removing candidates (pencil marks).

It starts with either two parallel rows or two parallel columns. Blocks are not involved here.

If you can find a row that contains the same pencil mark in exactly two spots, as well as another parallel row that mirrors it — containing the same pencil mark in only the same two spots, then you can use this information to eliminate similar pencil marks in the columns passing through those spots.

I know…that's a mouthful. Let me illustrate. Here we see a row containing exactly two 4s:

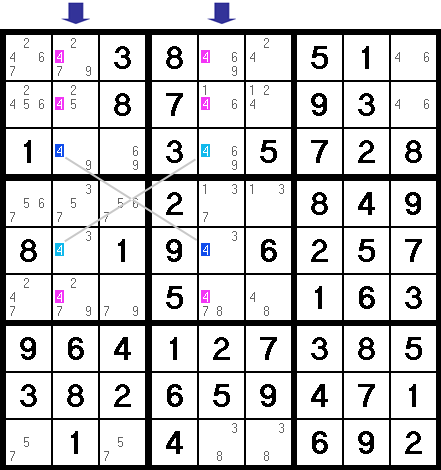
Next, if we zoom out a bit, we can see that another row, two rows down, has the same two 4s, and in the same two spots:

Now if we think about this, we know that each of these rows has to have a 4, right? And we also know the 4s cannot be on top of each other, because that would put two 4s in the same column.

Because of this, we can safely assume that either the light blue cells or the dark blue cells must be 4s.

Armed with this, let's zoom out all the way and shift our focus to the columns involved here (indicated with arrows below). Based on what we said above, the 4s in these columns must exist where these two rows cross - that is, where the blue 4s are.

Knowing that, all other 4s in the columns are not possible, and can be erased (erase all the pink 4s).

Again, this is one of those hard to find methods. In Sudoklue, the same pencil mark highlighting feature that helps me find hidden singles and omissions, can make X Wings easier to spot as well.

Of course, this whole concept can be rotated. If you can find two columns with only two identical positions for a given pencil mark, then the corresponding rows intersecting these positions can have all other candidates safely removed.

Next →


footer for X Wing page